题文

一种液体饮料采用圆柱体铝罐密封（易拉罐）包装．从外面量得圆柱的底面周长是18.84厘米，圆柱的高是12厘米．罐身上注明“净含量：355毫升．”请通过计算分析说明是否存在商家的欺骗行为？

题型：解答题  难度：中档

答案

[3.14×（18.84÷3.14÷2）2]×12， =[3.14×9]×12， =28.26×12， =339.12（立方厘米）， =339.12毫升． 339.12＜355， 答：通过计算说明商家存在欺骗行为．

据专家权威分析，试题“一种液体饮料采用圆柱体铝罐密封（易拉罐）包装．从外面量得圆柱的底..”主要考查你对  圆柱的表面积，圆柱的体积  等考点的理解。关于这些考点的“档案”如下：

圆柱的表面积圆柱的体积

考点名称：圆柱的表面积

• 圆柱的表面积公式：
  圆柱的表面积=圆柱的侧面积+两个底（圆）面积=2πrh+2π。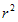
  
  表面积=侧面积+2个底面积
  侧面积=底面周长×高=3.14×直径×高=3.14×半径×2×高= 2πrh
  底面积=π×半径×半径=2π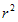

考点名称：圆柱的体积

• 圆柱的体积公式：
  v:体积 h:高 s:底面积 r:底面半径 c:底面周长
  (1)侧面积=底面周长×高
  (2)表面积=侧面积+底面积×2
  (3)体积=底面积×高（即v=sh)
  (4)底面积=半径×半径×3.14
  圆柱的体积=底面积×高即：v=sh=πr²h。