题文
| 把一个棱长为30分米的正方体削成一个最大的圆柱体.削去部分的体积是多少立方分米? |
答案
30×30×30-3.14×(
=27000-3.14×225×30, =27000-21195, =5805(立方分米), 答:削去部分的体积是5805立方分米. |
据专家权威分析,试题“把一个棱长为30分米的正方体削成一个最大的圆柱体.削去部分的体积..”主要考查你对 圆柱的表面积,圆柱的体积 等考点的理解。关于这些考点的“档案”如下:
圆柱的表面积圆柱的体积
考点名称:圆柱的表面积
- 圆柱的表面积公式:
圆柱的表面积=圆柱的侧面积+两个底(圆)面积=2πrh+2π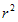 。
。
表面积=侧面积+2个底面积
侧面积=底面周长×高=3.14×直径×高=3.14×半径×2×高= 2πrh
底面积=π×半径×半径=2π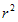
考点名称:圆柱的体积
圆柱的体积公式:
v:体积 h:高 s:底面积 r:底面半径 c:底面周长
(1)侧面积=底面周长×高
(2)表面积=侧面积+底面积×2
(3)体积=底面积×高(即v=sh)
(4)底面积=半径×半径×3.14
圆柱的体积=底面积×高即:v=sh=πr2h。





