题文

把一个圆柱形木块削成一个和它等底等高的圆锥体，体积减少了______．

题型：填空题  难度：偏易

答案

根据题干分析可得：削出的最大的圆锥的体积是圆柱的体积的 1 3 ， 所以削去部分的体积减少了：1- 1 3 = 2 3 ． 故答案为： 2 3 ．

据专家权威分析，试题“把一个圆柱形木块削成一个和它等底等高的圆锥体，体积减少了____..”主要考查你对  圆柱的表面积，圆柱的体积  等考点的理解。关于这些考点的“档案”如下：

圆柱的表面积圆柱的体积

考点名称：圆柱的表面积

• 圆柱的表面积公式：
  圆柱的表面积=圆柱的侧面积+两个底（圆）面积=2πrh+2π。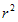
  
  表面积=侧面积+2个底面积
  侧面积=底面周长×高=3.14×直径×高=3.14×半径×2×高= 2πrh
  底面积=π×半径×半径=2π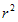

考点名称：圆柱的体积

• 圆柱的体积公式：
  v:体积 h:高 s:底面积 r:底面半径 c:底面周长
  (1)侧面积=底面周长×高
  (2)表面积=侧面积+底面积×2
  (3)体积=底面积×高（即v=sh)
  (4)底面积=半径×半径×3.14
  圆柱的体积=底面积×高即：v=sh=πr²h。