题文

如图A、B、C是三块长方形的铁片，请你选择一块做成一个如图那样的圆柱形铁盒（单位：厘米，铁盒的接口部分忽略不计） ①要求材料既够用而损耗率又最低的那块铁片是______． ②用这块铁片做成圆柱形铁盒后，材料的损耗率约是多少？（计算过程得数满百的保留整百数，不满百的保留整数；材料损耗率百分号前面的数保留一位小数）．

题型：解答题  难度：中档

答案

（1）因为圆柱的高是16厘米， 圆柱的周长是：2×3.14×4=25.12（厘米）， 而圆柱形的铁盒是有盖的， 所以要求材料既够用而损耗率又最低的那块铁片是C， （2）铁盒2个底面积2×3.14×4×4， =6.28×16， ≈100（平方厘米）， 铁盒的侧面积：2×3.14×4×16， =6.28×16×4， =100.48×4， ≈400（平方厘米）， 长方形的面积：33×24≈800（平方厘米）， 材料的损耗率约是（800-100-400）÷800×100%， =300÷800×100%， =37.5%， 答：材料的损耗率约是37.5%， 故答案为：C．

据专家权威分析，试题“如图A、B、C是三块长方形的铁片，请你选择一块做成一个如图那样的..”主要考查你对  圆柱的表面积，圆柱的体积  等考点的理解。关于这些考点的“档案”如下：

圆柱的表面积圆柱的体积

考点名称：圆柱的表面积

• 圆柱的表面积公式：
  圆柱的表面积=圆柱的侧面积+两个底（圆）面积=2πrh+2π。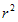
  
  表面积=侧面积+2个底面积
  侧面积=底面周长×高=3.14×直径×高=3.14×半径×2×高= 2πrh
  底面积=π×半径×半径=2π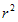

考点名称：圆柱的体积

• 圆柱的体积公式：
  v:体积 h:高 s:底面积 r:底面半径 c:底面周长
  (1)侧面积=底面周长×高
  (2)表面积=侧面积+底面积×2
  (3)体积=底面积×高（即v=sh)
  (4)底面积=半径×半径×3.14
  圆柱的体积=底面积×高即：v=sh=πr²h。