题文

有A、B两个圆柱形的容器，从里面量得A、B容器的底面周长分别为62.8cm、31.4cm，A、B内分别盛4cm和29cm深的水，先将B容器的一些水倒入A容器，使得两个容器水一样深，这时水深______cm．

题型：填空题  难度：中档

答案

（1）A容器的底面半径是：62.8÷3.14÷2=10（厘米）， 水的体积是：3.14×102×4， =3.14×100×4， =1256（立方厘米）， B容器的底面半径是31.4÷3.14÷2=5（厘米）， 水的体积是：3.14×52×29， =3.14×25×29， =2276.5（立方厘米）， 所以两个容器内水的体积之和是：1256+2276.5=3532.5（立方厘米）， （2）设两个容器内的水深为x厘米，则： 3.14×102×x+3.14×52×x=3532.5 314x+78.5x=3532.5 392.5x=3532.5 x=9 答：此时水深是9厘米． 故答案为：9．

据专家权威分析，试题“有A、B两个圆柱形的容器，从里面量得A、B容器的底面周长分别为62..”主要考查你对  圆柱的表面积，圆柱的体积  等考点的理解。关于这些考点的“档案”如下：

圆柱的表面积圆柱的体积

考点名称：圆柱的表面积

• 圆柱的表面积公式：
  圆柱的表面积=圆柱的侧面积+两个底（圆）面积=2πrh+2π。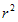
  
  表面积=侧面积+2个底面积
  侧面积=底面周长×高=3.14×直径×高=3.14×半径×2×高= 2πrh
  底面积=π×半径×半径=2π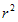

考点名称：圆柱的体积

• 圆柱的体积公式：
  v:体积 h:高 s:底面积 r:底面半径 c:底面周长
  (1)侧面积=底面周长×高
  (2)表面积=侧面积+底面积×2
  (3)体积=底面积×高（即v=sh)
  (4)底面积=半径×半径×3.14
  圆柱的体积=底面积×高即：v=sh=πr²h。